我々はCTR（クリック率）モデルをトレーニングすると、時々、私たちはこのctrを計算する際のインプレッションバイアスを回避するにはどうすればよいですか？
#(click)
ctr = ----------------
#(impressions)
のように私たちは、インプレッション数は、calculted小さすぎる、ということを知って、履歴データから実際のCTRをcalcute必要ctrは現実的ではありません。そこで、十分な大きさのインプレッションを除外するためのしきい値を常に設定しています。
しかし、私たちは、インプレッションが高いほど、ctrの信頼度が高いことを認識しています。それから私の質問は：ctrを計算するためのインプレッション正規化統計メソッドがありますか？
ありがとうございます！
推定されるctrの信頼区間の表示が必要な場合があります。 Wilson score intervalは試してみるといいです。あなたが信頼性スコアを計算する統計を下回る必要がある
：
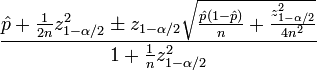
\hat pを観察CTR（#impressions対#clickedの割合）nは感想zα/ 2は、(1-α/2)標準の分位数でもなくMAL分布Pythonで単純な実装は、私はz（1-α/ 2） = 1.96、95％信頼区間に対応する使用、以下に示されています。コードの最後に3つのテスト結果を添付しました。
# clicks # impressions # conf interval
2 10 (0.07, 0.45)
20 100 (0.14, 0.27)
200 1000 (0.18, 0.22)
ここで、計算された信頼区間を使用するためのしきい値を設定できます。
from math import sqrt
def confidence(clicks, impressions):
n = impressions
if n == 0: return 0
z = 1.96 #1.96 -> 95% confidence
phat = float(clicks)/n
denorm = 1. + (z*z/n)
enum1 = phat + z*z/(2*n)
enum2 = z * sqrt(phat*(1-phat)/n + z*z/(4*n*n))
return (enum1-enum2)/denorm, (enum1+enum2)/denorm
def wilson(clicks, impressions):
if impressions == 0:
return 0
else:
return confidence(clicks, impressions)
if __name__ == '__main__':
print wilson(2,10)
print wilson(20,100)
print wilson(200,1000)
"""
--------------------
results:
(0.07048879557839793, 0.4518041980521754)
(0.14384999046998084, 0.27112660859398174)
(0.1805388068716823, 0.22099327100894336)
"""
これを2項パラメータとして扱う場合は、ベイジアン推定を行うことができます。前回のctrが均一（パラメータ（1,1）のベータ版）の場合、後ろはベータ（1 +＃クリック、1 +＃インプレッション - ＃クリック）です。あなたの後部平均は、この後部の単一の要約統計量が必要な場合は、＃click + 1 /＃impressions + 2ですが、おそらくそうではありません：
あなたの方法がctrは十分高いですが、ctr> 0.9のすべてに興味があるとしましょう。次に、ベータ分布の累積密度関数を使用して、確率マスのどの割合が0.9のしきい値を上回っているかを調べることができます（これはちょうど1 - 0.9のcdfです）。このようにして、サンプルのサイズが限られているため、あなたのしきい値には推定値の不確実性が組み込まれます。
この信頼区間を計算する多くの方法があります。 Wilsonスコアの代わりに、Clopper-Perrson間隔があります。これはスプレッドシートで役に立つとわかりました。
B()逆ベータ分布alphaある 信頼水準誤差（95％信頼レベルのために、例えば、アルファは5％です）
nは、sampの数レズ（例えば、インプレッション）xはB()の実装がBETA.INV式によって提供されるExcelで成功回数（例えばクリック）あります。
GoogleシートでBには同等の式は、（）はありませんが、Google Appsスクリプトのカスタム関数は、（JSTATため例えば検索githubの）あなたの答えのための
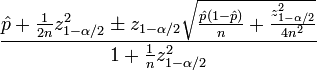
おかげでJavaScriptの統計ライブラリから適合させることができます。しかし、私は、推定されたctrに対する信頼ではなく、インプレッション - 正規化された統計的方法があるかどうかを知りたい。たとえば、この方法は次のようになります。＃（クリック）* 2 /（＃（インプレッション）+ avg（＃インプレッション）） – Tim
実際、私はあなたが何を望んでいるのか、なぜそのようにしたいのか分かりません。ベイジアン見積もりはどうですか？またはIMDBスコアのようなもの？ http://en.wikipedia.org/wiki/Bayes_estimator – greeness
z = 1.6は90％信頼に対応していませんか？ Googleのヘルパー：https://www.google.ru/search?q=z+values+confidence、ダミーの記事:-)：http://www.dummies.com/how-to/content/finding-appropriate- zvalues-for-given-confidence-l.html – skaurus