回転した矩形を描く

Question

これは数学的な問題のほうが多いかもしれません。

私の長方形の線を描くには、角を解決する必要があります。 私は、定義された幅と高さを持つ（x、y）に矩形中心を持っています。上に非回転長方形の青い点を見つけるために

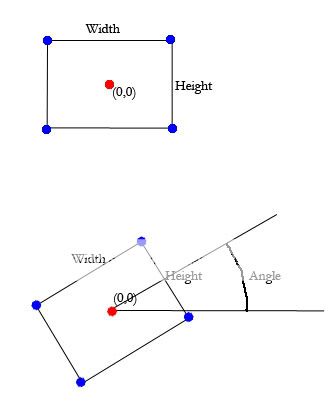
（角度= 0） それはどうすればよい

UL = (x-Width/2),(y+height/2)
UR = (x+Width/2),(y+height/2)
LR = (x+Width/2),(y-height/2)
LL = (x-Width/2),(y-height/2)

あります私は角度が0でない場合、ポイントを見つける？

ありがとうございます。

---

更新：私の写真には中心点として（0,0）がありますが、中心点はその位置にない可能性が最も高いです。

x' = x.cos(theta) - y.sin(theta) 
y' = x.sin(theta) + y.cos(theta) 

すなわち

| cos(theta) -sin(theta) | 
| sin(theta) cos(theta) | 

回転点が原点にない場合、減算：

Answer 1

まず= YY 0,0

X '= XX

Y' に中心点を変換

そして

の角度に対して回転

X '' =（Xx）* cosA - （Yy）* sinA

Y '=（Y-Y）* A +（X-X）*罪COS再びXに中心点をバック変換

、Y

X ''」=（X-X）* COS - （YY）*罪A + X

Y ''」=（Y-Y）* COS A +（X-X）*罪A + Y

したがって、以下で（X、Y）のすべての4点について計算（Xx）* cosA - （Yy）* sinA + x

Y '' 'Y =（Y-Y）* COS A +（X-X）*罪A +

のx、yは矩形の中心点であり、X、Yは、nを有する コーナー点である

'私がコメントに書いたようにAngleが0のときコーナーポイントでも正しく定義されています。

あなたは

UL = x + (Width/2) * cos A - (Height/2) * sin A , y + (Height/2) * cos A + (Width/2) * sin A 
UR = x - (Width/2) * cos A - (Height/2) * sin A , y + (Height/2) * cos A - (Width/2) * sin A 
BL = x + (Width/2) * cos A + (Height/2) * sin A , y - (Height/2) * cos A + (Width/2) * sin A 
BR = x - (Width/2) * cos A + (Height/2) * sin A , y - (Height/2) * cos A - (Width/2) * sin A 

を取得する代わりにした後、私は、これはあなたのソリューションに合ったと思います。

Answer 2

「シータ」は回転の反時計回りの角度である場合には、回転行列であります元の座標からの回転の中心、上記のように回転を実行し、回転の中心を再び戻します。 http://en.wikipedia.org/wiki/Transformation_matrix

Answer 3

での他の変換の例があります

これを実行する最も簡単な方法の1つは、回転前のポイントの位置を取り、その後、座標変換に適用することです。それは（0,0）を中心としていますので、これは単に用いた場合である：

X '= X COS（シータ） - Y罪（シータ）

Y' = Y COS（シータ）+ X sin（theta）

Answer 4

2D Rotationを参照してください。

q = initial angle, f = angle of rotation. 

x = r cos q 
y = r sin q 

x' = r cos (q + f) = r cos q cos f - r sin q sin f 
y' = r sin (q + w) = r sin q cos f + r cos q sin f 

hence: 
x' = x cos f - y sin f 
y' = y cos f + x sin f 

Answer 5

Rotation matrix

Answer 6

使用この（これはよくある質問となってきている）....私は、角度が0であるときは、正しくも、コーナーポイントを定義していない...

ctx.moveTo(defaults.x1, defaults.y1); 

    // Rotation formula 
    var x2 = (defaults.x1) + defaults.lineWidth * Math.cos(defaults.rotation * (Math.PI/180)); 
    var y2 = (defaults.y1) + defaults.lineWidth * Math.sin(defaults.rotation * (Math.PI/180)); 

    ctx.lineTo(x2, y2); 

    x2 = (x2) + defaults.lineHeight * Math.cos((defaults.rotation + 90) * (Math.PI/180)); 
    y2 = (y2) + defaults.lineHeight * Math.sin((defaults.rotation + 90) * (Math.PI/180)); 
    ctx.lineTo(x2, y2); 

    x2 = (x2) + defaults.lineWidth * Math.cos((defaults.rotation + 180) * (Math.PI/180)); 
    y2 = (y2) + defaults.lineWidth * Math.sin((defaults.rotation + 180) * (Math.PI/180)); 
    ctx.lineTo(x2, y2); 

    x2 = (x2) + defaults.lineHeight * Math.cos((defaults.rotation + 270) * (Math.PI/180)); 
    y2 = (y2) + defaults.lineHeight * Math.sin((defaults.rotation + 270) * (Math.PI/180));