は、どのように私は、次の手順を合計することができますシーケンスを合計する方法は?
#include <iostream>
int main()
{
int n;
std::cin>>n;
unsigned long long res=0;
for (int i=1;i<=n;i++)
{
res+= n/i;
}
std::cout<<res<<std::endl;
return 0;
}
あなたはこれよりもよりよい解決策を知っていますか:
⌊n/1⌋ + ⌊n/2⌋ + ⌊n/3⌋ + ... + ⌊n/n⌋
これは単純にC++でのO(n)のソリューションですか?私はO(1)またはO(log(n))を意味します。ありがとうございました:)と解決策
編集: ありがとうございました。誰かが溶液Oを希望する場合(SQRT(N)): パイソン:
import math
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
n = int(input())
print(seq_sum(n))
C++:大nについて
#include <iostream>
#include <cmath>
int main()
{
int n;
std::cin>>n;
int sqrtn = (int)(std::sqrt(n));
long long res2 = 0;
for (int i=1;i<=sqrtn;i++)
{
res2 +=2*(n/i);
}
res2 -= sqrtn*sqrtn;
std::cout<<res2<<std::endl;
return 0;
}


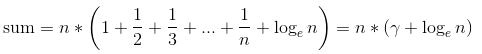
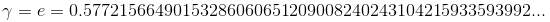
 は超越番号です。)
は超越番号です。)
 時間解決策を提供するはずです。
時間解決策を提供するはずです。
'O(sqrt(n))'は問題ありませんか? – kraskevich
@ILoveCoding:O(1)ではないにもかかわらず、回答として投稿することができます。それが正しければ、私は1つはそれをupvoteだろう。 – NPE
これは 'O(1)'の解決策と非常に関係しているようです:http://math.stackexchange.com/questions/740442/how-do-i-evaluate-this-suminvolving-the-floor-function – Alec