私はRed-Black Treesについてのwikiを読んでいました。ノードは赤か黒のどちらかであるレッドブラックツリー - ブラック高さ制限
：
は、誰かが第五制限について詳しく説明することはできます。
根は黒です。
すべての葉（NIL）は黒です。 （すべての葉は根と同じ色です）
赤いノードの両方の子はすべて黒です。
任意のノードからその子孫の葉までのすべての単純なパスには、同じ数の黒いノードが含まれます。
the final case of insertion（ウィキ上ケース5）は私たちを与えた後、例RBTの状態を与えられたので、私はそれを理解することの困難を抱えている：
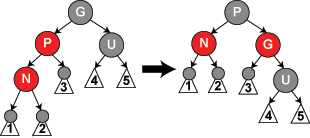
はありません4と5をい1,2、および3よりも黒いノードがもう1つありますか？
1,2,3,4および5はすべてサブツリーです。我々は木1,2および3のルートノードの色が黒であることを知っている。この挿入ケースは、（挿入ケース3からの）新しく挿入されたノードの祖父母であった一部のNで再帰的に呼び出された可能性があるため、ノード1-5のいずれかが葉ノードであるかどうかわからない。
サブツリー1,2および3はすべてブラックノード（G before、P after）の下にあり、サブツリー4および5は2つのブラックノード（GおよびUの前、PおよびU ）。サブツリー1,2および3には、サブツリー4および5よりも黒いノードがもう1つあります。
それをもっと見ると、私はこれと一緒に行くつもりです。 1,2,3,4、および5は、それ自体が葉ではなく、独自のサブツリーです。 NとGには黒い子（1,2,3の頭）があるので、そこから出てくるすべてのパスは、以前と同じように黒ノードの数が同じであったため、実際には変化しません。前にUを通過したすべてのパスはUとGを黒ノード（2つ）としていたので、すべてのパスがUとPの黒ノード（2つ）を通過しなければなりませんでした。これは以前と同じ数のブラックノードです。したがって、制約は、それらの下のサブツリーに保持されていると仮定して、依然として保持されます。 – bunnybare
さらに、サブツリー1,2、および3には4と5よりも黒いノードがもう1つあります。これは、4と5がUを通過して1,2と3に一致する黒いノードを追加するためです。 今すぐ入手してください。 – bunnybare
私はそれを深く読んだだけで、画像に問題があるようです。 Nので
はそれが最後insert前P未満の子供[1,3]または[2,3]が存在した（インサートは敬意2又は1であった）ことを意味する挿入されたノードです。したがって、最後の挿入の前に、PとUは赤でなければなりません（そして4,5は黒です）。
Wiki図を解読していただきありがとうございます。間違っているのではなく、あいまいではありません。
ページの「トーク」タブには、「三角形は葉ではなくサブツリーを表現するものではありません。一部のサブツリーは、そのルートが黒でなければならないことを示す黒い円が上部にあります。
円がない三角形は、ルートノードの色とツリーの深さが分からない（おそらく無関係な）サブツリー（葉を含む）を表しているようです。
したがって、図は単に「ルール5」に違反しているかどうかを示すのに十分な情報を提供していません。私たちはそうではないと考えるようにしなければなりません。
いいえ、1と2と3はブラックノードであり、4と5はそうではないため、5つのパスすべてに2つのブラックノードがあるためです。 –
@IanMcMahon どのように4と5は黒ではありませんか？彼らは制限3のためになるはずですか？ – bunnybare
確かそうですね、それじゃない。ウィキが間違っているかどうか疑問に思ったことがあります。ウィキは間違っていますか？それは世界の強固さを信じている！ –